搜索结果: 1-12 共查到“数学 Nature”相关记录12条 . 查询时间(0.189 秒)
六磷酸肌醇（又名植酸），简称InsP6，广泛存在于植物中，是种子磷素的主要储存形式，对植株体内磷稳态的维持具有重要作用[1-4]。作物种子中的InsP6无法被人体和动物吸收利用，其大量存在反而会大幅降低肠道对矿质营养元素等无机营养和蛋白质等有机营养的吸收效率，同时这些植酸磷随后通过粪便排入环境造成水体富营养化等问题[5-6]。因此，培育低种子InsP6含量的农作物品种对改善作物营养品质和保护生态环...
浙江大学尹勋钊、卓成等在《Nature Communications》发文报道首个基于铁电存算一体芯片的组合优化求解器框架（图）
浙江大学 尹勋钊 卓成 Nature Communications 存算一体 芯片 组合优化 求解器框架
2024/8/7
组合优化问题在现实生活中具有广泛的应用场景（如物流、资源分配、金融、交通）。这类问题通常属于非确定性多项式时间难题（NP-hard），具有极高的计算复杂度。目前，基于传统冯·诺伊曼体系架构的组合优化问题求解器的芯片尺寸、成本随问题规模呈指数性增长，性能和求解能力则指数性下降，因此亟需探索更加高效的组合优化问题专用芯片，这也是美国国防部去年发布的2.38亿美元微电子计划重点方向之一。近日，浙江大学尹...
国家自然科学基金委员会南大杜瑞瑞团队在《Nature》发文揭示一种新型的玻色子分数量子霍尔态（图）
杜瑞瑞 量子 拓扑 理论
2024/11/20
美国麻省大学艾姆赫斯特分校（Tigran Sedrakyan副教授）、北京大学（杜瑞瑞教授）组成的合作团队在电子-空穴关联系统中激子拓扑序的研究方面取得了重要进展。 该工作在理论上提出了关联激子由于阻挫效应导致强量子涨落所产生的玻色子拓扑序的新机制；实验上在电子-空穴浓度不平衡的InAs/GaSb量子阱中观察到了通过激子形成的时间反演对称破缺的新型拓扑态。实验与理论相结合，首次揭示了激子系统中的玻...
2022年10月6日，中国科学院分子细胞科学卓越创新中心（生物化学与细胞生物学研究所）陈玲玲研究员受邀在Nature Methods上发表了题为“Towards higher-resolution and in vivo understanding of lncRNA biogenesis and function”的主题评论，重点论述了新技术的应用为长非编码RNA研究带来的前沿进展以及今后研究的...
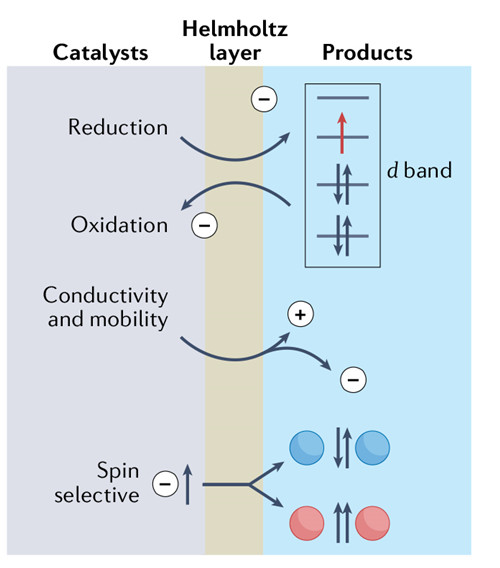
拓扑材料是过去十多年凝聚态物理领域的明星材料之一，研究者们追求其拓扑非平庸的表面态及无耗散的电子传输，并试图在超导技术、量子计算及低能耗器件上实现应用。然而，由拓扑特性导致的表面化学性质一直缺乏相关研究，这也极大限制了人们对拓扑材料的认知与应用。中国科学院宁波材料技术与工程研究所李国伟研究员长期致力于拓扑材料的设计生长与催化应用，系统研究了拓扑绝缘体（Journal of Energy Chemi...
近日，华南理工大学数学学院计算生物研究团队的最新研究成果在国际著名学术期刊Nature Communications上发表。该成果提出了基于非线性动力学的时空信息变换理论与具有对称结构的自动储备池计算框架。该框架直接将观测到的高维动态信息转化为储备池，把高维空间数据映射到目标变量的未来时间信息，通过同时求解一对共轭的时空信息转换方程，获得目标变量时间序列中的未知值，从而实现快速、多步地预测目标变量...
A symplectic structure on a manifold is a closed nondegenerate exterior 2-
form. The most common type of symplectic structure arises on a complex
manifold as the imaginary part of a Hermitian metr...
THE LOCAL NATURE OF HYPOTHESIS TESTS INVOLVING INEQUALITY CONSTRAINTS IN NONLINEAR MODELS
Hypothesis testing multivariate nonlinear one-sided tests nonlinear in- equality constraints tests
2015/7/31
This paper derives several properties unique to nonlinear model hypothesis testing
problems involving linear or nonlinear inequality constraints in the null or alternative
hypothesis. The paper is...
Urban chaos and replacement dynamics in nature and society
bifurcation chaos fractal dimension logistical map replacement dynamics Volterra-Lotka’s model urbanization
2011/7/7
Many growing phenomena in both nature and society can be predicted with sigmoid function. The growth curve of the level of urbanization is a typical S-shaped one, and can be described by using logisti...
True nature of long-range order in a plaquette orbital model
Rigorous results in statistical mechanics Classical phase transitions
2010/12/9
We analyze the classical version of a plaquette orbital model that was recently introduced and studied numerically by S. Wenzel and W. Janke.
True nature of long-range order in a plaquette orbital model
Rigorous results in statistical mechanics Classical phase transitions
2010/12/16
We analyze the classical version of a plaquette orbital model that was recently introduced and studied numerically by S. Wenzel and W. Janke.
The Fundamental Lemma is a somewhat obscure combinatorial identity introduced by Robert P. Langlands [L79] as an ingredient in the theory of auto-morphic representations.